Analysis of variance (ANOVA)
Contents
Analysis of variance (ANOVA)¶
Recommended reading¶
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. Freely available online at www.biostathandbook.com
Analysis of variance: test for a statistically significant difference between means of 3+ different groups
Does not tell you which group is different
Requires the use of post hoc analysis to determine which means are different from each other
Example:
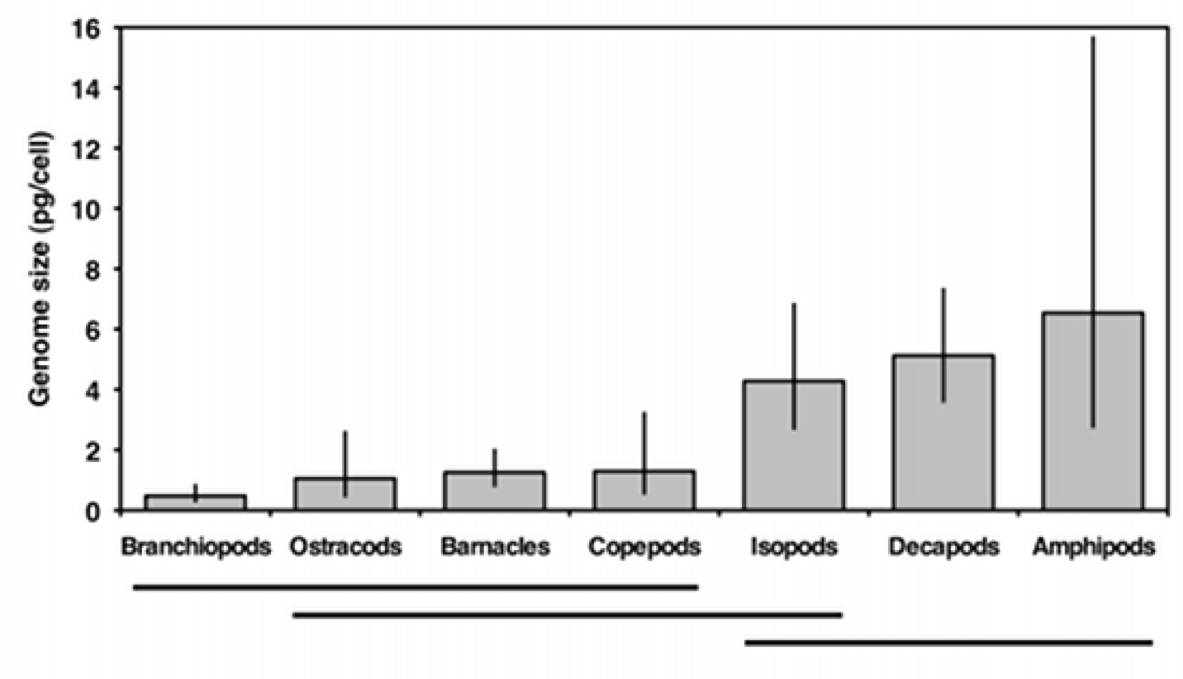
One-Way ANOVA Fisher’s LSD post-hoc test used to determine which populations are different from each other.
Two-Way ANOVA Data are grouped into different genotypes, within those groupings, sex is segregated. Thus two factors are varying across the examples
One-Way example:
J Populations (or “treatments”)
N samples per population
\(H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4\)
\(H_a\): One mean will be different from any of the others
Three different types of CTDs in a water bath, each has four different measurements (does not require the same number of samples within each population)
Use the F-statistic: The ratio of the variances of two groups of samples taken from a normal distribution follows an F distribution
The F distribution can be used to test whether variances are significantly different. In the case of ANOVA, we want to test whether the variance of differences between different groups is larger than the variance within groups.
Sum of Squares Between: SSB = \(\sum_{j=1}^J{N_j(\bar{y_j}-\bar{y})^2}\) where \(\bar{y_j}\) is the mean of each population and \(\bar{y}\) is the mean of all samples
Mean Square Between: MSB = \(\frac{SSB}{J-1}\)
\(J-1\) is the degrees of freedom in calculating MSB.
Sum of Squares Within: SSW = \( \sum_{j=1}^J{\sum_{i=1}^{N_j}}({y_{ij}} - \bar{y}_j)^2\)
Mean Square Within: MSW = \( \frac{SSW} {(\sum_{j=1}^J { N_j}) -J }\)
\(\sum_{j=1}^J ({ N_j} -J )\) is the degrees of freedom in calculating MSW. This is the total number of samples minus the number of groups.
F-Distribution: \(F =\frac{MSB}{MSW}\)
The null hypothesis can be rejected if F is large. This is a one-tailed test, since small values of F do not lead to a rejection of the null hypothesis. The region of rejection is is above some critical level, which is determined by the confidence level and the degrees of freedon in the numerator and denominator.
Popular post-hoc tests¶
Fisher’s LSD (least significant difference)
Tukey HSD (honest significant difference)