Multidimensional Scaling Analysis
Contents
Multidimensional Scaling Analysis¶
Multidimensional scaling analysis (MDS) provides a visual representation of similarity between samples that have multiple variables. MDS is built on the idea of a distance matrix that quantifies the dissimilarity between samples.
Euclidean Distance¶
How far away two points are when plotted as \(x\),\(y\) coordinates.
For three variables, the distance between two samples (\(i\) and \(j\)) can be visualized in three-dimensional space.
\(d_{ij} =||X_i-X_j|| = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2 + (z_i-z_j)^2}\)
if \(X_i = (x_{i}, y_{i}, z_{i})\)
Bray Curtis Distance¶
Often used for identifying differences in community composition based on abundance. If \(u\) and \(v\) represent two different samples of counts of different groups, the Bray Curtis distance is:
\(d= \frac{\Sigma|u_i-v_i|}{\Sigma(u_i+v_i)}\)
if \(u\) and \(v\) are positive, then 0 < d < 1
Example¶
In this example, \(u\), \(v\) and \(q\) are three different samples, in which four different groups are counted.
import numpy as np
from scipy.spatial import distance
u = [415,200,310,411]
v = [615,100,330,203]
q = [614,101,331,202]
data = np.array([u,v,q])
print(data)
[[415 200 310 411]
[615 100 330 203]
[614 101 331 202]]
data.T # Transpose so that each column represents a sample
array([[415, 615, 614],
[200, 100, 101],
[310, 330, 331],
[411, 203, 202]])
# compute distances between points
dist = distance.pdist(data,'braycurtis')
dist
array([0.20433437, 0.20433437, 0.00160256])
# represent distances as a matrix
distmatrix = distance.squareform(dist)
distmatrix
array([[0. , 0.20433437, 0.20433437],
[0.20433437, 0. , 0.00160256],
[0.20433437, 0.00160256, 0. ]])
Other measures of distance¶
Python can be used to compute a variety of different distance measures.
https://docs.scipy.org/doc/scipy/reference/spatial.distance.html
For an excellent resource on the applications of different distance calculations in ecology, including appropriate measures for binary (presence/absence) data, see A Primer of Ecological Statistics by Gotelli and Ellison.
Types of multidimensional scaling analysis¶
classical MDS
Also known as Torgerson MDS or principal coordinate analysis (PCoA)
The distance matrix is converted to a similarity matrix. Once this is done, the same steps as PCA are performed:
compute eigenvectors and eigenvalues
same as PCA for Euclidean distances
Steps:
create a data matrix
compute a dissimilarity matrix, D, with elements \(d_{ij}\)
transform the dissimilarity matrix \(d^*_{ij} = \frac{1}{2}d^2_{ij}\)
center the dissimilarity matrix \(\delta^*_{ij} = d^*_{ij}-\bar{d}^*_{i}-\bar{d}^*_{j}+\bar{d}^*\)
compute the eigenvectors and eigenvalues
if the dissimilarity index is euclidean distance, this is mathematically equivalent to PCA
Non-metric (iterative) MDS
preserves rank of distance
minimizes stress
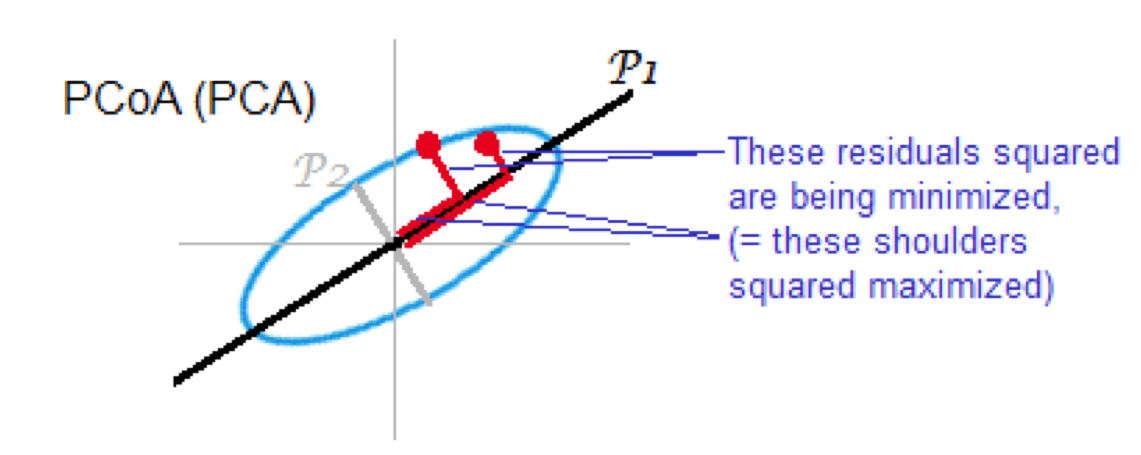
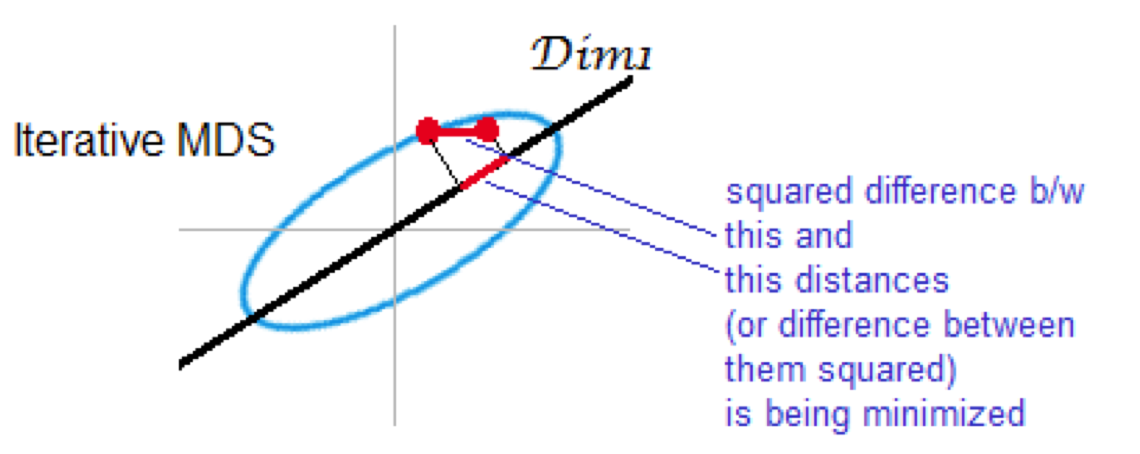
Summary of comparison of PCA and MDS¶
PCA - based on Euclidean distances, good for data without strong skew & data without outliers
PCoA - use when other distance measures are appropriate equivalent to PCA when Euclidean distances used
Non-metric multidimensional scaling (NMDS) - preserves ran order of distance rather than actual values (similar to many non-parametric statistics. One reason for using this type of analysis is that it is less sensitive to outliers.
ANOSIM and PermANOVA¶
determine whether groups of samples are significantly different
are distances WITHIN the groups smaller than the differences BETWEEN groups
Implementing MDS in Python¶
Compute distance matrices
Includes PCA functions
Includes PCoA (metric MDS based on distance matrix)
Does not include non-metric MDS
Includes PermANOVA for assessing statistically significant differences
Computes distance matrices
Includes general MDS function (metric or non-metric)
Includes related analyses such as linear discriminant analysis